제1회 초콜릿컵 에디토리얼

• 시간 복잡도: 테케당 $O(1)$
• 키워드: 수학, 제곱의 합 공식
• 출제 의도: 초반 포지션에 쓸 쉬운 문제로 가장 먼저 떠오른 문제

이 계산을 $O(1)$에 하기 위해, $a = \min(R, C)$, $b = |R-C|$라고 합시다. 그러면 $b$는 모든 층에 대해 상수임을 알 수 있고, 원하는 합은 다음과 같이 계산 가능합니다.

$$ \begin{align} White &= \sum^{a}_{i=1}{2i(i+b) - (i+(i+b)) + 1} \\ &= \sum^{a}_{i=1}{2i^2 + 2(b-1)i + 1 - b} \\ &= \frac{a(a+1)(2a+1)}{3} + (b-1)a(a+1) + a(1-b) \end{align} $$

$$ \begin{align} Dark &= \sum^{a}_{i=1}{2i(i+b) - (i+(i+b))} \\ &= White - a \end{align} $$

모든 나눗셈은 나누어 떨어지고 $a,b \le 10^6$일 때 64bit 정수형으로 overflow 없이 계산되므로 이 식을 그대로 코드로 옮기면 됩니다.

위의 Part 1에서 나이브 루프를 짜면 TLE를 받는다고 설명을 드렸는데, 이는 언어와 컴파일러에 따라 사실이 아닐 수 있습니다(!). LLVM 기반 컴파일러(C/C++(clang), Rust)를 사용하면 제곱의 합, k제곱의 합 같은 고정된 형태뿐 아니라 recurrence chain이라는 형태로 해석 가능한 루프라면 모두 $O(1)$인 코드로 최적화를 해 준다고 하네요.

Godbolt, 관련 설명 블로그 글 (영어)

검수 중에 이 현상을 발견하고 저와 검수진이 다 같이 충격을 받았습니다. 이 문제는 에디토리얼 업로드와 함께 불판에도 올라갈 예정입니다.

• 시간 복잡도: $O(1)$
• 키워드: 애드 혹
• 출제 의도: 초반 포지션에 문제를 내려고 짜내고 짜내다 보니 애드혹이 되어버림(…)

일단 크게 두 가지 상황으로 나눠 볼 수 있습니다. $X=0$ or $Y=0$ or $X=Y$이면 ㅋ나이트가 갈 수 있는 곳이 4곳이고, 아니라면 일반 나아트처럼 8곳입니다. 전자의 경우 예시 정답처럼 (또는 45도 돌려서) 똑같이 움직여주면 정답이 됩니다. 이 때 이동 횟수는 7입니다.

후자의 경우, 어떤 지점 $A$를 골라서 $A$에서 이동 가능한 8곳을 모두 막아야 합니다. $A$에서 1스텝에 갈 수 있는 지점 중 아무 두 곳을 $B$와 $C$라고 할 때, $B \rightarrow A \rightarrow C$처럼 $B$에서 $C$로 2스텝에 갈 수 있는 경로가 항상 존재합니다. 또한 $B$와 $C$가 서로 반대편이 아니라면, 선분 $BC$에 대한 $A$의 거울상 $A’$가 존재해서 $B \rightarrow A’ \rightarrow C$라는 두 번째 경로가 존재합니다. $(0,0)$에서 1스텝에 갈 수 있는 지점을 $A$로 고르면 시작하자마자 8곳 중 하나를 막고 시작하게 되므로, 나머지 7곳을 각각 2스텝에 밟고 마지막에 $A$로 진입하면 15회의 이동으로 게임을 끝낼 수 있습니다.

임의의 $A$의 이웃 $B,C$에 대해, $B$와 $C$ 사이의 최소 스텝 수가 2임($\hArr$ $B$에서 $C$로 1스텝에 갈 수 없음)을 증명하는 방법은 여러 가지가 있습니다.

• 정수/기하 웰노운 증명: 1스텝에 갈 수 있다면 $ABC$가 격자점 정삼각형이 되는데, 그런 정삼각형은 존재하지 않는다.
• 홀짝성 증명 (by wider93): $X,Y$가 서로소일 때 홀짝성은 둘 다 홀수이거나 하나만 홀수인데, 2스텝을 이동하면 전자는 (짝수, 짝수)가 되고 후자는 좌표의 합의 홀짝성이 달라져서 (aka 체스판 색칠) 2스텝 이동한 곳과 1스텝 이동한 곳이 일치할 수 없다.

위의 내용을 굳이 증명하지 않고 그래프 탐색으로 짜는 방법도 있습니다. 이웃을 모두 막을 점 $A$를 하나 정하고, $A$의 모든 이웃들의 방문 순서에 대해 최단 경로를 탐색하는 방법입니다.

• $A$의 이웃의 쌍 $B,C$에 대해서 $A$를 거치지 않고 $B$에서 $C$로 가는 최단 경로를 BFS로 찾는다.
• $A$의 이웃들을 방문하는 모든 가능한 순서에 대해서 최단 경로의 길이의 합을 최소화하는 경로를 구한다.

이렇게 2단계로 나누지 않고 매번 경로 탐색을 시도한다면 $B$와 $C$가 서로 반대편일 때 최악 $8^4$회의 탐색을 해야 하기 때문에 TLE를 받을 수도 있습니다.

• 시간 복잡도: $O(C(N))$, $C(N)$은 $N$번째 카탈란 수 (= 올바른 괄호 문자열의 개수)
• 키워드: 브루트포스, 재귀
• 출제 의도: 이런 복잡도를 가진 문제를 아직 본 적이 없어서 내 보기로 함

최악의 경우 $N=15$이므로 초콜릿의 개수는 총 30개이고, 30칸을 흑백으로 채우는 방법의 수는 $2^{30} \approx 10^9$입니다. 이대로 가면 TLE를 받겠네요.

전체 칸 수는 30칸이지만 화이트 초콜릿, 다크 초콜릿의 개수가 각각 15개로 고정되어 있습니다. 이들을 배열하는 방법의 수는 $\binom{30}{15} \approx 1.5 \times 10^8$입니다. 여전히 1초에 계산하기는 빡세고, 예쁜 초콜릿인지 판별도 해야 하기 때문에 역시 TLE를 받을 것 같습니다. (열심히 커팅하면 될 수도 있겠지만…)

이 문제를 시간 내에 해결하려면 정확히 예쁜 초콜릿에 대해서만 계산을 해야 합니다. 예쁜 초콜릿의 정의를 잘 읽어보면 올바른 괄호 문자열의 조건과 일치함을 알 수 있으며, 따라서 계산해야 하는 경우의 수는 $C(15) = \binom{30}{15} \div 15 \approx 10^7$입니다.

모든 올바른 괄호 문자열을 생성하는 한 가지 방법으로, 현재 몇 개의 괄호를 사용했고 열린 괄호가 몇 번인지를 유지해서 재귀를 짜면 왼쪽부터 오른쪽의 순서로 문자열을 완성할 수 있습니다. 그리고 앞의 문자열이 정확히 어떻게 생겼는지는 상관이 없이 현재의 계산값 ($\mod 10^5$)만 유지해 주면 중복계산을 최소화하여 모든 최종값들을 얻을 수 있습니다.

앞의 풀이에서 “현재 몇 개의 괄호를 사용했고 열린 괄호가 몇 번인지를 유지” 부분을 DP로 관리할 수도 있습니다.

• DP table table[a][b][n]: a개의 괄호를 사용, b개의 열린 괄호가 있는 상황에 중간값으로 n이 될 수 있는가를 나타내는 bool 값

(원래 풀이는 Python set을 사용했지만 시간 복잡도를 조금 더 명확히 하기 위해 boolean table로 수정했습니다.)

이 경우 시간 복잡도는 $O(n^2 \operatorname{mod})$이고, 상수 1/4이 붙으므로 (a*b 테이블에서 반쪽 삼각형만 사용하고, a와 b의 홀짝이 항상 같음) 연산량은 약 $5 \times 10^6$이 됩니다.

• 시간 복잡도: $O(\max(N) + T)$ (로그 추가된 풀이도 허용)
• 키워드: DP, 경우의 수 나누기
• 출제 의도: “초콜릿” 테마의 메인 문제 중 하나

$N$이 홀수이므로, $3 \times N$ 격자를 아래와 같이 체스판으로 칠하면 O가 X보다 1개 많습니다. 따라서 구멍을 하나 빼고 도미노로 나누려면 구멍의 위치가 O인 경우만 가능하고, X인 경우는 답이 0입니다.

OXOXOX ... XO
XOXOXO ... OX
OXOXOX ... XO

O인 경우 중에서도 윗줄이나 아래 줄인 경우 (대칭성), 가운데 줄인 경우로 나눌 수 있습니다.

1. 구멍이 윗줄인 경우

... OOOOXOOOO ...
... OOOABOOOO ...
... OOOCDOOOO ...

A칸과 B칸 사이의 경계선을 생각해 봅시다. 경계선을 긋는다면 (A와 B가 서로 다른 도미노에 속한다면) 면적의 홀짝성에 의해 C와 D 사이에도 경계선을 그어야 합니다. 반대로 경계선이 없다면 (A와 B가 하나의 도미노라면) 같은 논리에 의해 C와 D도 하나의 도미노여야 합니다. 후자의 경우 A의 위에 하나의 도미노를 추가로 확정할 수 있습니다.

따라서 이 경우의 답은 아래 그림에서 “A를 채우는 경우의 수 × B를 채우는 경우의 수 + C를 채우는 경우의 수 × D를 채우는 경우의 수” 입니다.

... AAAA XBBBB ...
... AAAA BBBBB ...
... AAAA BBBBB ...

... CCxx XDDDD ...
... CCCxx DDDD ...
... CCCxx DDDD ...

2. 구멍이 가운데 줄인 경우

... OOOABCOOO ...
... OOOOXOOOO ...
... OOODEFOOO ...

이 경우에도 면적 홀짝성을 사용하면 AB와 EF 도미노를 놓거나, BC와 DE 도미노를 놓는 두 가지 경우로 나눌 수 있습니다. 이 때 이 두 가지 상황은 서로 대칭이므로, 이 경우의 답은 아래 그림에서 “E를 채우는 경우의 수 × F를 채우는 경우의 수 × 2” 입니다.

... EEE xx FFFF ...
... EEEE X FFFF ...
... EEEE xx FFF ...

이제 2133. 타일 채우기에서 썼던 점화식을 적용해서 최대 $N$값까지 memoization해놓고 각각의 입력에 대해 필요한 값을 가져와서 $O(1)$에 계산해서 답을 내면 됩니다.

참고로 세그 풀이도 생각해볼 수 있지만 이 풀이는 적어도 17424. 2xN 타일링과 쿼리 (Diamond 4) 이상으로 보입니다.

• 시간 복잡도: 상관 없음
• 키워드: 구현 많음, Flood Fill or Union-Find
• 출제 의도: “초콜릿” 테마의 메인 문제 중 하나 (실제 있는 퍼즐 장르)

구체적으로 체크해야 하는 부분을 나열하면 다음과 같습니다.

1. 퍼즐이 영역으로 잘 나누어졌는가? (불필요한 경계선이 없는가?)
2. 각 영역이 정확히 하나씩의 흰색과 회색 영역을 포함하는가?
3. 두 색깔의 모양이 정확히 일치하는가?
4. 주어진 수가 있을 때, 두 색깔의 면적과 일치하는가? 같은 영역에 수가 2개 이상 있지는 않은가?

출제자의 풀이에서는 각각을 다음의 방법으로 구현했습니다.

1. 각 좌표를 돌면서, 아직 처리하지 않은 칸에서 시작해서 답지에 대해 Flood Fill을 돌리면서 불필요한 경계선을 체크한다.
2. 1의 결과를 가지고 1과 같은 방법으로 색깔에 대해 Flood Fill을 돌린다. 각 색깔을 시작점으로 하는 Flood Fill의 횟수가 1,1인지 확인한다.
3. 2에서 얻은 흰색과 회색의 좌표의 집합에 대해 canonicalize를 적용해 일치하는지 확인한다.
4. 1의 과정에서 현재 영역에 들어 있는 모든 수를 모아서, 수가 1개 이하인지, 1개라면 면적이 맞는지 확인한다.

일부 검수자 분들은 Flood Fill 대신 Union-Find를 사용하였고, canonicalize 대신 한쪽 색깔은 그대로 두고 반대쪽 색깔만 돌리고 뒤집어서 같은 모양인지 확인하는 방법을 사용하였습니다.

• 시간 복잡도: 테케당 $O(1)$
• 키워드: 애드 혹
• 출제 의도: “초콜릿” 테마의 메인 문제 중 하나
  • 원래 보스 문제로 기획하였으나, 문제를 만들다 보니 Proof by AC 할만한 문제가 되어서 예상 난이도가 하향 조정되는 불상사(?)가 있었습니다…

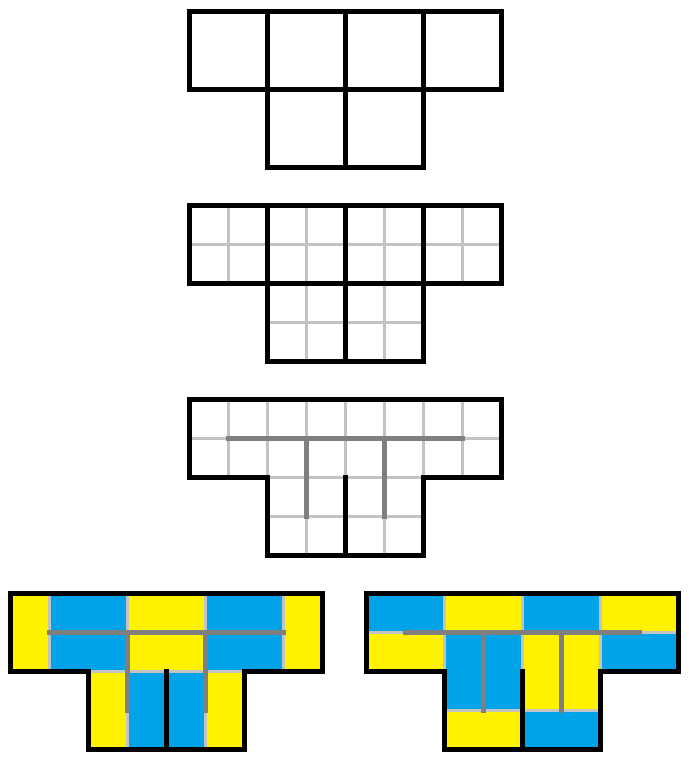
일단 주어진 $M \times N$ 직사각형을 체스판 모양으로 칠합니다. 그러면 각각의 도미노는 항상 흰색 칸과 검은색 칸을 하나씩 차지하게 됩니다. 남아있는 흰색 칸의 개수를 $W$, 검은색 칸의 개수를 $B$라고 하면 놓을 수 있는 도미노의 최대 개수는 $\min(W,B)$입니다.

이제 구멍의 개수 $K$와 각각의 구멍의 색깔로 case work을 해 봅시다.

• $K=0$
  • $M$과 $N$이 모두 4의 배수(=짝수)이므로 가로나 세로 중 한 방향으로 도미노를 깔면 됩니다. 답은 $\frac{MN}{2}$입니다.
• $K>0$, 구멍의 색깔이 모두 같을 때
  • 이 경우 $\min(W,B) = \frac{MN}{2} - K$입니다. 그만큼의 도미노를 실제로 놓는 방법은 $K=0$의 해에서 시작해서 구멍을 포함하는 도미노를 모두 제거하면 됩니다.
• $K=2$, 흰색과 검은색이 하나씩 제거되었을 때
  • 항상 $\frac{MN}{2}-1$개의 도미노를 놓을 수 있습니다. 증명은 아래 “명제 1 증명"을 참조하세요.
• $K>2$, 흰색과 검은색 중 한쪽은 1개, 다른 쪽은 $K-1$개 제거되었을 때
  • 위의 2번째 경우와 동일한 논리로, $\min(W,B) = \frac{MN}{2} - (K-1)$개의 도미노를 놓을 수 있습니다.
• $K=4$, 흰색과 검은색이 2개씩 제거되었을 때
  • 이 문제의 꽃이라고 할 수 있습니다. 결론부터 말씀드리면 거의 항상 $\frac{MN}{2} - 2$개의 도미노를 놓을 수 있고, 구석 1칸이 구멍에 의해 격리된 상황일 때만 답이 $\frac{MN}{2} - 3$개가 됩니다. 증명은 아래 “명제 2 증명"을 참조하세요.
  • 구석이 격리된 경우는 그 구석 옆의 칸 중 하나 $H$가 구멍이 아니라고 생각하면 (1,2)인 상황이 되는데, 이 상황은 위에서 설명했듯이 $\frac{MN}{2} - 2$개의 도미노를 놓을 수 있으며, 여기서 $H$를 포함하는 도미노를 제거하면 됩니다.

흰색과 검은색이 1개씩 제거된 경우에 대한 증명입니다.

주어진 직사각형의 모든 칸을 가로지르는 해밀턴 회로를 생각합니다. $M$과 $N$이 모두 짝수이므로 이러한 해밀턴 회로는 항상 존재합니다. 예를 들면 아래와 같이 지그재그 모양으로 길을 만들면 됩니다.

+-+-+-+-+-+-+
|           |
+ +-+-+-+-+ +
| |   |   | |
+ + + + + + +
| | | | | | |
+ + + + + + +
| | | | | | |
+ + + + + + +
| | | | | | |
+ + + + + + +
|   |   |   |
+-+-+-+-+-+-+

여기서 흰색과 검은색 칸을 하나씩 제거하면 1개 또는 2개의 경로가 만들어지는데, 이 경로를 따라 도미노를 놓으면 됩니다.

흰색과 검은색이 2개씩 제거된 경우에 대한 증명입니다. 기본적으로 Puzzling SE의 Jaap님의 풀이를 따르며, 논리를 단순화하기 위해 일부 각색하였습니다. 다른 증명도 있으니 궁금하시면 링크에 들어가서 읽어보시는 것도 좋습니다.

명제 1 증명과 비슷한 방법을 사용하는데, 이번에는 주어진 직사각형을 $2 \times 2$ 크기의 정사각형 단위(이하 “블럭”)로 생각합니다.

Lemma 1. 블럭을 단위로 한 polyomino가 주어집니다. 여기서 아무 흰색과 검은색 칸을 하나씩 제거했을 때, 남아있는 도형은 항상 도미노 타일링이 존재합니다.

Proof. 명제 1을 증명할 때처럼 해밀턴 회로를 사용합니다. 아래 그림처럼 polyomino의 spanning tree를 아무거나 하나 정하면 그에 따른 단위 사각형 칸들의 해밀턴 회로가 만들어지므로, 명제 1의 논리를 사용하여 결론이 증명됩니다.

이제 원래의 문제로 돌아가서, 아래처럼 블럭 단위의 해밀턴 회로를 그려놓고 블럭에 구멍이 뚫릴 수 있는 경우들을 생각해 봅시다.

여러 개의 구멍을 포함한 블럭이 없다면, 위의 해밀턴 회로를 두 개의 경로로 나누어서 B 구멍과 W 구멍을 하나씩 포함하도록 할 수 있음을 어렵지 않게 알 수 있습니다. 이렇게 나누어진 두 경로는 Lemma 1에 의해 도미노 타일링이 존재하므로, 전체 직사각형 또한 타일링이 존재합니다.

그렇다면 다른 경우는 어떨까요?

1. 4개의 블럭을 포함하는 블럭이 있다면, 그냥 그 블럭을 지우고 직사각형의 나머지 부분을 한 방향의 도미노로 채우면 됩니다.
2. 3개의 구멍을 포함한 블럭 $X$가 있고 그 블럭의 남은 칸을 포함하는 도미노를 놓을 수 있다면, 해당 도미노를 놓은 후의 상황을 Lemma 1의 상황으로 재해석할 수 있습니다. 예를 들어 3개의 구멍의 색깔이 BBW라면, 직사각형에서 $X$를 뺀 도형을 블럭 polyomino로 보고, 원래 빠져야 할 두 번째 W 구멍과 추가로 놓은 도미노가 차지한 B를 구멍으로 보면 됩니다.
3. 2개의 구멍을 포함한 블럭이 있고 두 구멍의 색이 다르다면 (BW), 그 블럭에 도미노를 하나 놓으면 비슷하게 Lemma 1로 환원됩니다.
4. 2개의 구멍의 색이 같다면, 위의 3개 구멍의 경우와 비슷하게 도미노를 2개 추가합니다. 일반성을 잃지 않고 구멍의 색을 BB라고 합시다. 위의 해밀턴 회로의 상황에서 생각해보면, 블럭이 하나 제거되어 해밀턴 경로가 되었고, B 구멍 2개가 경로의 양 끝에 위치해 있으므로, 두 W 구멍 사이 어딘가를 나누어서 여전히 Lemma 1 조건을 만족하는 두 개의 경로를 만들 수 있습니다. 이는 WW가 또 다른 하나의 블럭에 위치하더라도 여전히 성립합니다.

위의 2번과 4번의 경우, 추가되는 도미노가 블럭 해밀턴 회로를 따라서 놓여야 한다는 제한이 있습니다. 이는 남아있는 칸 중 하나가 ㄴ자 코너의 구석에 있으면 불가능한데, 이 코너가 직사각형의 실제 코너가 아니라면 다른 해밀턴 경로(e.g. 위 그림을 90/180/270도 회전한 것)를 선택함으로써 회피할 수 있습니다.

• 시간 복잡도: $O(N)$
• 키워드: DP using connection profile
• 출제 의도: 커넥션 프로파일이 된다는 것을 이해하면 복잡한 구현을 하지 않더라도 풀 수 있도록 함

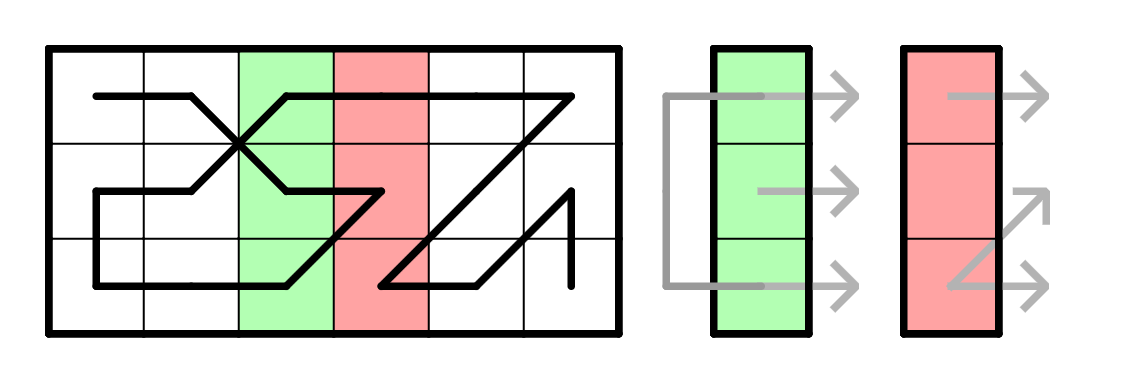
커넥션 프로파일이란, 어떤 중간 state를 연결 요소의 상태로 나타내서 그러한 상태들간의 전이를 이용해 DP를 하는 것을 말합니다. jh05013님의 블로그 글에 그림과 함께 잘 설명되어 있으니 참고로 읽어보시면 좋을 것 같습니다.

보통의 커넥션 프로파일 문제는 칸 수가 가변이어서 state의 연결 요소를 관리하는 다량의 구현이 들어가는데, 이 문제는 세로 칸 수가 고정이고 이 수가 작기 때문에(3), column 단위로 state를 모델링하면 이러한 구현을 피할 수 있습니다.

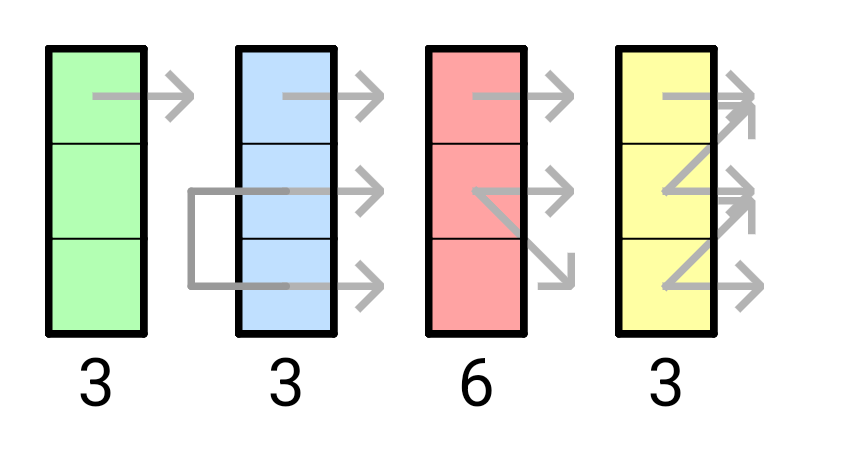
예를 들면, 위의 첫 번째 그림과 같은 경로가 있을 때, 초록색 column까지 보면 오른쪽의 초록색 형태로 요약이 가능하고, 빨간색 column까지 보면 빨간색의 형태로 요약이 가능한 식입니다.

이런 식으로 state를 만들면 다음과 같은 관찰이 가능합니다.

• 3칸 중 한 칸은 시작 칸과 연결되어 있어서 단독으로 오른쪽 화살표 하나가 나와야 한다.
• 나머지 칸은 서로 연결되어서 화살표가 하나씩 나오거나, 단독으로 0개 또는 2개가 나와야 한다.

이 조건을 만족하는 state는 아래처럼 총 15가지로 추릴 수 있습니다.

이제 state간의 transition은 손으로 세도 되고 (그렇게 많지 않습니다), 코드를 짜서 구해도 됩니다. 한 가지 문제는 이렇게 하면 시작 부분이 깔끔하게 state로 표현되지 않는데, 이 부분은 연습문제로 남깁니다.

아쉬운 점은 검수 때 푸신 분들이 모두 너무 정석적으로 푸셨다는 점이네요. (blood sweat tears ㅋㅋ…)

• 키워드: 구현, esolang
• 출제 의도: 개인적으로 재미있게 생각했던 Piet이라는 언어를 알리고 싶어서…

주어진 문제가 그닥 어렵지 않기 때문에, 초콜릿 언어의 기본적인 사용법 몇 가지만 알아내면 어렵지 않게 루프를 구성해서 풀 수 있습니다.

• 프로그램 종료 커맨드가 따로 없기 때문에, 영역을 잘 만들어서 프로그램을 종료하는 방법부터 찾아야 합니다. 가장 작은 영역으로 종료하려면 크기 3의 영역을 사용할 수 있으며, 아래와 같이 구성하면 됩니다.

-->abcdZ
      ZZ

       Z
-->abcdZ
       Z

• $DP$ 변화를 시도하는 방향 때문에 루프는 항상 우회전을 하도록 (시계 방향) 짜는 것이 가장 쉽습니다. 좌회전을 하려고 하면 유턴을 해버리는 함정이 있습니다. 좌회전을 강제하려면 아래와 같이 이동 규칙에 의한 출구를 하나만 만들면 됩니다.

x
xdcba<--
x
y
z

• if를 넣거나 while을 탈출하려면 D 또는 C를 반드시 써야 합니다. 딱히 어느 쪽이 더 쓰기 쉽다 같은 건 없는 것 같습니다.
• 같은 커맨드를 그냥은 연속으로 쓸 수 없기 때문에 (하나의 영역으로 처리됨), 두 커맨드 사이에 dp 같은 유사 no-op을 끼워넣어야 합니다.
• 큰 면적의 P를 만들 때 출구에 주의합니다.

이 문제의 “초콜릿” 프로그래밍 언어는 제가 만든 언어이긴 하지만 완전한 창작은 아니고, 상당 부분 Piet을 기반으로 하고 있습니다. Instruction pointer의 진행 방식은 완전히 동일하며, $DP$와 $CC$라는 용어도 여기서 유래합니다.

이 언어를 문제로 내는 데 있어서 가장 큰 걸림돌은 소스 코드가 그림 파일(!)이라는 점, 그리고 커맨드가 한 영역의 색깔이 아니라 두 영역의 색깔의 차이로 결정된다는 점이었는데요. 둘 다 쓸데없이 코딩을 어렵게 만든다는 점이 가장 컸고, 기본적으로 그림 파일을 백준에 제출할 수도 없기 때문에, Piet을 그대로 문제로 내지 않고 Piet의 커맨드들을 아스키 문자로 매핑을 시켜서 영역의 글자 기반으로 커맨드가 실행되도록 했습니다.

Piet 원본에 no-op 커맨드가 없기 때문에 초콜릿 언어에도 no-op을 넣지 않았는데, 이로 인해 2개의 커맨드를 연속으로 실행을 할 수 없게 되었고, 우회 방법을 찾아야 하는 새로운 허들이 생겼습니다. 저는 이를 나름 재미있는 점이라고 생각해서 그대로 두었고, 이 문제의 검수를 진행해 주셨던 sait2000님과 jh05013님도 (“왜 nop 없어요 ㅂㄷㅂㄷ” 외에는…) 특별한 코멘트를 주시지 않아서 그대로 문제가 나가게 되었습니다.